BALANCE DE MATERIA EN YACIMIENTOS SATURADOS DE PETRÓLEO NATURALMENTE FRACTURADOS

Para la solución de la EBM se considera que un yacimiento fracturado puede modelarse utilizando propiedades diferentes para cada medio poroso (matriz y fractura) o con valores promedio para el sistema total, es por eso que se proponen técnicas de solución para cada una de estas suposiciones. Debido a los arreglos matemáticos realizados, la EBM permite realizar la estimación no solo de los volúmenes de petróleo y gas originales, sino también de la capacidad de almacenamiento relativa de los medios porosos y de la compresibilidad para los sistemas fracturado y total. El modelo en cuenta las siguientes consideraciones:

1. El yacimiento es un sistema isotérmico.
2. El yacimiento está compuesto por: roca naturalmente fracturada, agua producida,
petróleo fiscal y gas de superficie.
3. El yacimiento está compuesto de 4 fases: petróleo, gas, agua y roca naturalmente
fracturada.
4. El petróleo solo se encuentra en esta fase.
5. El gas existe como fase gaseosa y disuelto en el crudo.
6. El componente agua solo existe en fase acuosa y reduce el volumen poroso disponible a
hidrocarburos.
7. El componente roca solo existe en fase roca.
8. La roca tiene dos medios porosos en comunicación hidráulica: los poros y las fracturas.
9. El sistema matriz porosa y fractura son compresibles.
10. Yacimiento volumétrico y sin producción de agua.
11. No hay inyección de fluidos (agua y/o gas) al yacimiento.
12. La porosidad de la fractura, porosidad de la matriz y saturación de agua son
uniformes.
13. La presión de yacimiento es uniforme a lo largo del mismo, lo cual indica que no
hay gradientes de presión vertical u horizontal.
14. Yacimiento saturado

La EBM está dada por la siguiente expresión:

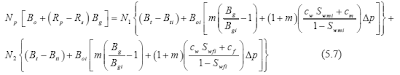en donde el primer termino representa el volumen total (gas y petróleo) que ocupa el espacio poroso en todo el sistema; el segundo término se refiere a el volumen de transferencia (crudo y gas) de matriz a fractura y el tercer término expresa la transferencia
de fluido (crudo y gas) de las fracturas a superficie.
Además:
en donde N1, N2 y Np es el volumen de petróleo (STB) original en la matriz, en las fracturas y de petróleo producido acumulado, respectivamente, cm es la compresibilidad promedio de la matriz, cf es la compresibilidad promedio de la fractura y cw es la compresibilidad del agua (psi-1).
El método de solución depende de cuáles incógnitas son conocidas y cuáles son consideradas como incógnitas.

CASO 0

Este considera el caso convencional de Havlena y Odeh (sin capa de gas) que consiste en reorganizar la ecuación para obtener grupos de variables de manera que se comporten como una línea recta al ser graficados, donde la EBM general es:

Luego, las variables son definidas como:
De modo que la EBM puede expresarse como:

donde Eo1 representa la expansión neta del petróleo original en el sistema matriz y Eo2 es la expansión neta del petróleo original en el sistema de fracturas. La anterior expresión puede escribirse como:

De modo que una gráfica de F/Eo1 vs. Eo2/Eo1 da una recta de pendiente N2 y corte N1 como ilustra la siguiente figura.
Luego, la EBM queda:

Como se conoce m, se tiene una expresión lineal de la forma y = a1 x1 + a2 x2 con:

que puede solucionarse por regresión lineal para N1 y N2. Una alternativa de este caso es realizar un gráfico que describa una línea recta en donde y/x2 es la variable dependiente de x1/x2, cuya pendiente es el petróleo original en la matriz y cuya ordenada es el petróleooriginal en las fracturas. Al tomar la ecuación lineal y hacer el cociente con la variable x2

CASO 2

Conociendo la capacidad de almacenamiento relativa en cada medio poroso, desconociendo el volumen de petróleo inicial, el tamaño de la capa de gas inicial y la compresibilidad. Esta suposición será aplicable en casos en los que la diferencia de compresibilidades sea pequeña o uno de los medios porosos predomine en capacidad de almacenamiento sobre el otro; la compresibilidad efectiva del medio poroso total (matriz y fracturas) se define como:
Como la capacidad de almacenamiento en las fracturas, relativa al almacenamiento total se define:
Luego, Cem-f se puede escribir:
Rescribiéndola , considerando que N = N1 + N2 , se tiene:
De esta manera, es posible aplicar el método de regresión lineal de la forma


Una vez conocidos y ,x1 , x2 y x3, se hallan los coeficientes a1, a2 y a3, a partir de los cuales se calculan las incógnitas de la siguiente forma:


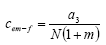Para la solución por regresión no lineal, la expresión de F puede ser escrita de manera que aparezcan todas las incógnitas posibles, de la siguiente forma

Esta ecuación puede ser solucionada mediante la utilización de regresión no lineal entre cualquier combinación de las variables N, γ, m y cef.

Fundamentos de Ingeniería de Yacimientos - Freddy H. Escobar, Ph.D.